DCCN lab program – To implement error detection and error correction techniques

Aim

To implement error detection and error correction techniques.

 

S/W required

Java

 

Background information

An error occurs when the output information does not match the input information. Digital signals suffer from noise during transmission, which can create errors in binary bits travelling from one system to another. That is, a 0 bit may become a 1 bit, or a 1 bit may become a 0.

 

Many factors, including noise and cross-talk, can contribute to data corruption during transmission. The top layers are unaware of real hardware data processing and work on a generic picture of network architecture. As a result, the top levels anticipate error-free transmission between the systems.

 

Most programs would not work normally if they received incorrect data. Voice and video applications, for example, may be unaffected and continue to work normally despite occasional problems.

 

Error detection

When a message is sent, it may be jumbled by noise or the data may be damaged. To avoid this, we employ error-detecting codes, which are bits of extra data appended to a digital message to assist us detect whether an error occurred during transmission. Some of the well-known error detection techniques are:

• Parity check
• Checksum
• Cyclic Redundancy Check (CRC)

 

Parity check

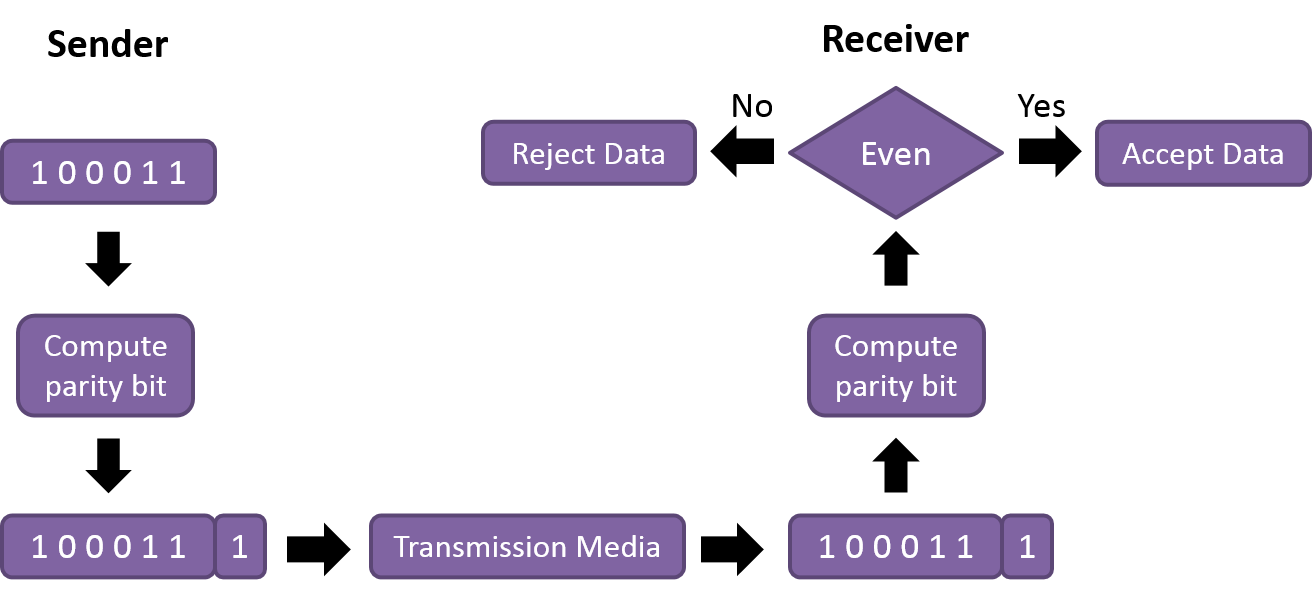
The process of error detection using even parity is illustrated as shown below:

 

One extra bit is transmitted in addition to the original bits to make the number of 1s even in the case of even parity or odd in the case of odd parity. While creating a frame, the sender counts the amount of 1s in it. If even parity is utilized and the number of 1s is even, one bit with the value 0 is added. In this manner, the number of 1s remains even. If the number of 1s is odd, a value 1 is added to make it even.

 

The receiver just counts how many 1s are in a frame. If the number of 1s is even and even parity is utilized, the frame is regarded as uncorrupted and approved. Even if the number of 1s is odd and odd parity is utilized, the frame is not damaged. The receiver can identify a single bit flip in transit by counting the number of 1s. However, when more than one bit is incorrect, it is extremely difficult for the receiver to identify the problem.

 

Checksum

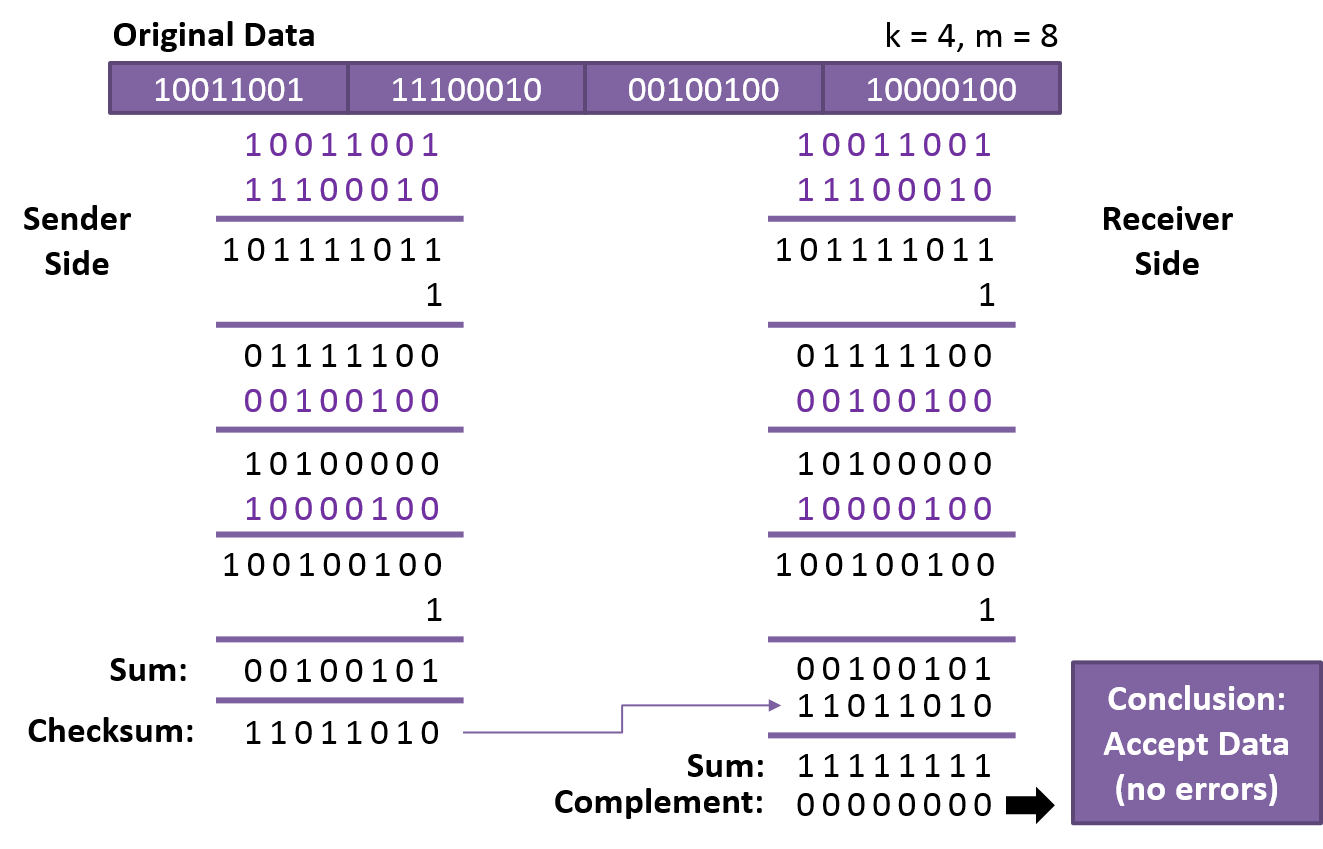
The process of error detection using checksum involves splitting the data into k segments of m bits. To get the sum, the segments are summed at the sender’s end using 1’s complement arithmetic. To obtain the checksum, a complement of the sum is taken. The checksum segment is sent with the data segments.

 

To obtain the sum, all received segments are summed using 1’s complement arithmetic at the receiver’s end. The sum is then calculated. If the result is 0, the data is accepted; otherwise, it is rejected. An example of error detection using checksum is shown below:

 

Cyclic Redundancy Check (CRC)

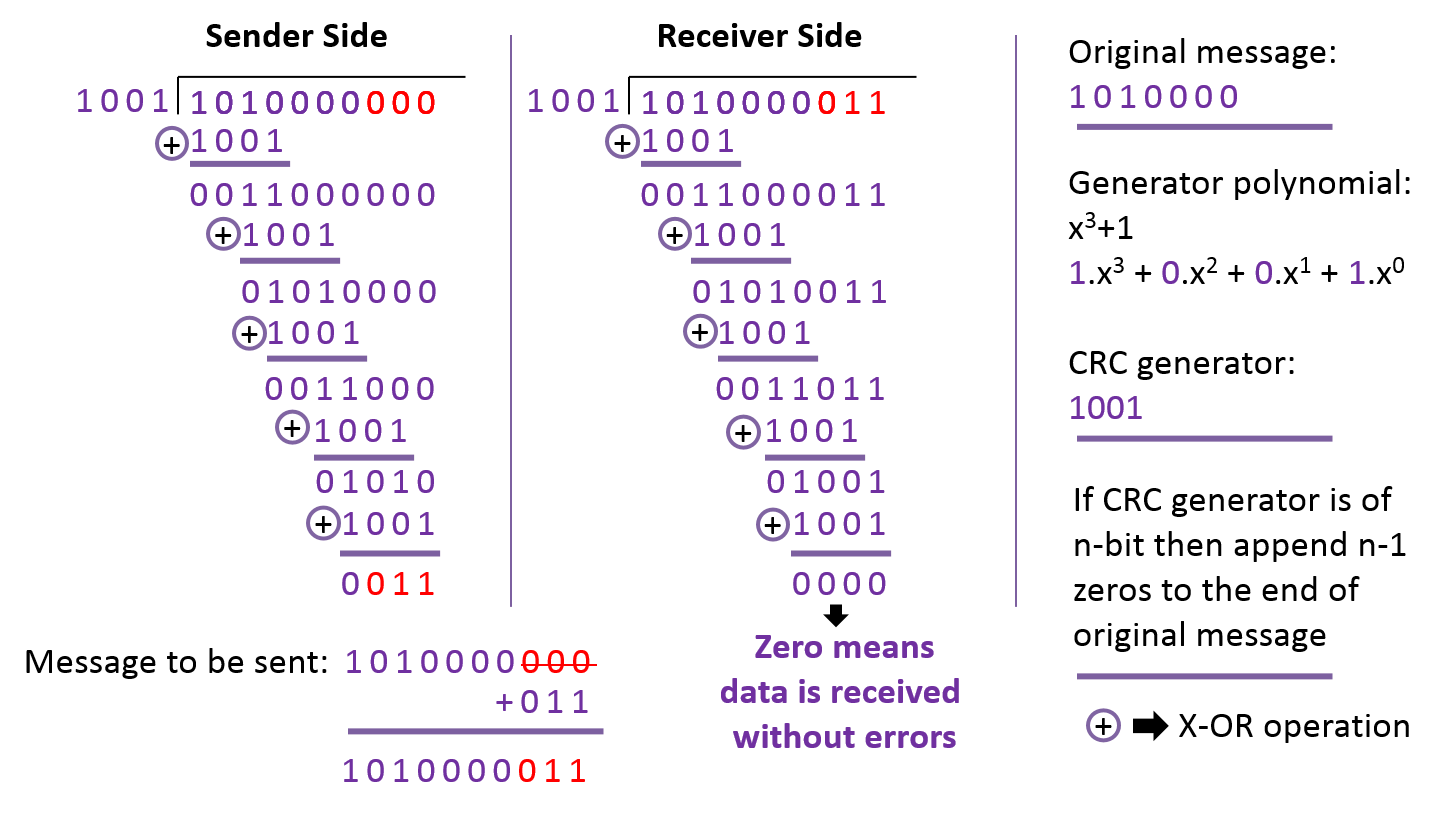
Unlike checksum scheme, which is based on addition, CRC is based on binary division. In CRC, a sequence of redundant bits, called cyclic redundancy check bits, are appended to the end of data unit so that the resulting data unit becomes exactly divisible by a second, predetermined binary number.

 

At the destination, the incoming data unit is divided by the same number. If at this step there is no remainder, the data unit is assumed to be correct and is therefore accepted. A remainder indicates that the data unit has been damaged in transit and therefore must be rejected. An example of error detection using CRC is shown below:

 

Error correction

Error Correction codes are used to detect and correct the errors when data is transmitted from the sender to the receiver.

 

Error Correction can be handled in two ways:

• Backward error correction: Once the error is discovered, the receiver requests the sender to retransmit the entire data unit.
• Forward error correction: In this case, the receiver uses the error-correcting code which automatically corrects the errors.

 

A single additional bit (ex: parity bit) can detect the error, but cannot correct it.

 

For correcting the errors, one has to know the exact position of the error. For example, if we want to calculate a single-bit error, the error correction code will determine which one of seven bits is in error. To achieve this, we have to add some additional redundant bits.

 

Suppose r is the number of redundant bits and d is the total number of the data bits. The number of redundant bits r can be calculated by using the formula:

 

The value of r is calculated by using the above formula. For example, if the value of d is 4, then the possible smallest value that satisfies the above relation would be 3.

 

To determine the position of the bit which is in error, a technique developed by R.W Hamming is Hamming code which can be applied to any length of the data unit and uses the relationship between data units and redundant units.

 

Hamming code

Parity bits: The bit which is appended to the original data of binary bits so that the total number of 1s is even or odd.

 

Even parity: To check for even parity, if the total number of 1s is even, then the value of the parity bit is 0. If the total number of 1s occurrences is odd, then the value of the parity bit is 1.

 

Odd Parity: To check for odd parity, if the total number of 1s is even, then the value of parity bit is 1. If the total number of 1s is odd, then the value of parity bit is 0.

 

Algorithm of Hamming code:

• An information of ‘d’ bits is added to the redundant bits ‘r’ to form d+r.
• The location of each of the (d+r) digits is assigned a decimal value.
• The ‘r’ bits are placed in the positions 1, 2, …, 2^k-1.
• At the receiving end, the parity bits are recalculated. The decimal value of the parity bits determines the position of an error.

 

Activity

Program: To implement error detection using even parity.

import java.util.*;
import java.io.*;
class Driver
{
	//Method to count number of ones in the data
	static int countOnes(int data[], int b)
	{
		int count = 0;
		for(int i=0; i<b; i++)
		{
			if(data[i] == 1)
				count++;
		}
		return count;
	}
	//Method to check whether the count is even or not
	static boolean isEven(int count)
	{
		if(count % 2 == 0)
			return true;
		else
			return false;
	}
	//Method to calculate the parity bit of received data
	static int checkEvenParity(int data[], int b)
	{
		int count = countOnes(data, b);
		int bit = 0;
		if(isEven(count) == false)
			bit = 1;
		else
			bit = 0;
		return bit;
	}
	public static void main(String[] args) throws IOException
	{
		System.out.println("How many bits you want to send? ");
		Scanner input = new Scanner(System.in);
		int b = input.nextInt();
		//One extra bit to store parity
		int data[] = new int[b+1];
		//Read input data
		System.out.println("Enter the bits, each bit must be separated by a space: ");
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		//Read input data as single line of text
		StringTokenizer bits = new StringTokenizer(br.readLine());
		int i = 0;
		//Extract each bit from the string
		while(bits.hasMoreTokens())
		{
			data[i] = Integer.parseInt(bits.nextToken());
			i++;
		}
		int count = countOnes(data, b);
		//Set the parity bit
		if(isEven(count) == false)
			data[b] = 1;
		else
			data[b] = 0;
		//Print the data
		System.out.println("Original data to be sent is: ");
		for(i=0; i<b+1; i++)
			System.out.print(data[i] + " ");
		//Read the bit position to change
		System.out.println("\nEnter the bit position to change it.");
		System.out.println("Position should be less than " + b + ": ");
		int pos = input.nextInt();
		if(data[pos] == 0)
			data[pos] = 1;
		else
			data[pos] = 0;
		//Print the data
		System.out.println("Data to be sent is: ");
		for(i=0; i<b+1; i++)
			System.out.print(data[i] + " ");
		//Check for even parity
		int bit = checkEvenParity(data, b);
		if(data[b] == bit)
			System.out.println("\nNo Errors. Data is accepted.");
		else
			System.out.println("\nError found. Data is corrupted.");
	}
}

 

Input and output:

How many bits you want to send?
5
Enter the bits, each bit must be separated by a space:
1 0 0 1 1
Original data to be sent is:
1 0 0 1 1 1
Enter the bit position to change it.
Position should be less than 5:
2
Data to be sent is:
1 0 1 1 1 1
Error found. Data is corrupted.

 

Program: To implement error detection using checksum.

import java.util.*;
class Driver
{
	//Code to complement the t value to get checksum
	static String complement(String sum, int m)
	{
		char bits[] = sum.toCharArray();
		for(int i=0; i<m; i++)
		{
			if(bits[i] == '1')
				bits[i] = '0';
			else
				bits[i] = '1';
		}
		return new String(bits);
	}
	static String calChecksum(String data[], int k, int m)
	{
		int a = Integer.parseInt(data[0], 2);
		int b = 0;
		int c = 0;
		//Code to add the segments in data array
		for(int i=1; i<k; i++)
		{
			b = Integer.parseInt(data[i], 2);
			c = a+b;
			String temp = Integer.toBinaryString(c);
			if(temp.length() > m)
			{
				temp = temp.substring(1);
				c = Integer.parseInt(temp, 2);
				c = c + 1;
			}
			a = c;
		}
		String sum = Integer.toBinaryString(c);
		//Code to insert 0's before the value in sum to make it 8 bits
		String t = sum;
		if(sum.length() < m)
		{
			int diff = m - sum.length();
			for(int i=0; i<diff; i++)
				t = "0" + t;
		}
		sum = t;
		return sum;
	}
	static boolean validateChecksum(String data[], int k, int m, String senderChecksum)
	{
		String sum = calChecksum(data, k, m);
		int s = Integer.parseInt(sum, 2);
		int sc = Integer.parseInt(senderChecksum, 2);
		s = s + sc;
		String finalsum = complement(Integer.toBinaryString(s), m);
		if(finalsum.indexOf('1') > -1)
			return false;
		else
			return true;
	}
	public static void main(String[] args)
	{
		System.out.println("How many segements of data? ");
		Scanner input = new Scanner(System.in);
		int k = input.nextInt();
		System.out.println("How many bits per segment? ");
		int m = input.nextInt();
		String data[] = new String[k];
		for(int i=0; i<k; i++)
		{
			System.out.println("Enter data segment " + (i+1) + ": ");
			data[i] = input.next();
		}
		String senderChecksum = complement(calChecksum(data, k, m), m);
		System.out.println("Sender side checksum value: " + senderChecksum);
		System.out.println("Which segment you want to change?");
		System.out.println("Enter a number less than " + k);
		int segment = input.nextInt();
		System.out.println("Data in the segment is: " + data[segment]);
		System.out.println("Which bit you want to change?");
		System.out.println("Enter a number less than " + m);
		int bit = input.nextInt();
		StringBuilder sb = new StringBuilder(data[segment]);
		if(sb.charAt(bit) == '1')
			sb.setCharAt(bit,'0');
		else
			sb.setCharAt(bit,'1');
		data[segment] = new String(sb);
		System.out.println("Data being sent to receiver is:");
		for(int i=0; i<k; i++)
		{
			System.out.print(data[i] + " ");
		}
		System.out.print("\n");
		if(validateChecksum(data, k, m, senderChecksum))
			System.out.println("Data received has no errors!");
		else
			System.out.println("Data received is corrupted!");
	}
}

 

Input and output:

How many segments of data?
4
How many bits per segment?
8
Enter data segment 1:
10011001
Enter data segment 2:
11100010
Enter data segment 3:
00100100
Enter data segment 4:
10000100
Sender side checksum value: 11011010
Which segment you want to change?
Enter a number less than 4
1
Data in the segment is: 11100010
Which bit you want to change?
Enter a number less than 8
1
Data being sent to receiver is:
10011001 10100010 00100100 10000100
Data received is corrupted!

 

Result

Error detection and correction techniques were explored and implemented successfully.

 
Visit DCCN video tutorials for more study material.